Ever heard the saying, “small things add up”? Well, what if those small things multiplied like crazy, growing bigger and faster every single day? Think a million dollars is a lot? Let’s talk about the power of a penny. One little copper coin, doubled every day for a month. Spoiler alert: it’s mind-blowing. We’ll explore how the “Penny Doubling Challenge” reveals the astonishing potential of exponential growth and what it means for your finances.
The Million-Dollar Question: Penny vs. $1,000,000
Imagine you’re given two options: a cool million dollars right now, or a single penny that doubles in value each day for 30 days. Which would you choose? Most people instinctively grab the million. It’s tangible, immediate wealth. But what if that humble penny could hold even greater potential?
The Penny’s 30-Day Transformation
Let’s break down the penny’s journey day by day and witness the magic of compounding:
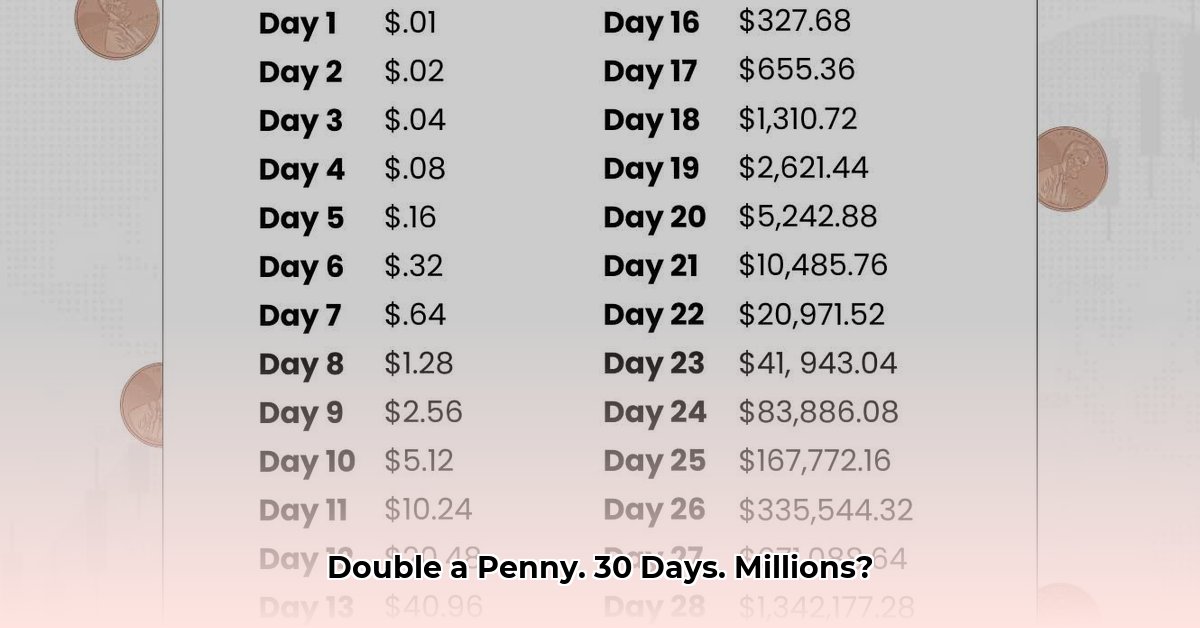
| Day | Amount |
|---|---|
| 1 | $0.01 |
| 2 | $0.02 |
| 3 | $0.04 |
| 4 | $0.08 |
| 5 | $0.16 |
| 6 | $0.32 |
| 7 | $0.64 |
| 8 | $1.28 |
| 9 | $2.56 |
| 10 | $5.12 |
| 11 | $10.24 |
| 12 | $20.48 |
| 13 | $40.96 |
| 14 | $81.92 |
| 15 | $163.84 |
| 16 | $327.68 |
| 17 | $655.36 |
| 18 | $1,310.72 |
| 19 | $2,621.44 |
| 20 | $5,242.88 |
| 21 | $10,485.76 |
| 22 | $20,971.52 |
| 23 | $41,943.04 |
| 24 | $83,886.08 |
| 25 | $167,772.16 |
| 26 | $335,544.32 |
| 27 | $671,088.64 |
| 28 | $1,342,177.28 |
| 29 | $2,684,354.56 |
| 30 | $5,368,709.12 |
Notice how the growth accelerates dramatically. This is the power of compounding in action.
Unraveling the Magic: Exponential Growth Explained
The penny’s explosive growth isn’t magic; it’s math. Compounding, a fundamental financial principle, is at play. Each day, the penny’s value doubles not just on the original cent, but on the accumulated amount from the previous day. This snowball effect is what fuels exponential growth. A simple graph visualizing this would show a curve starting flat and then sharply rising—a classic exponential growth pattern.
Why the Penny Wins: The Power of Compounding
So why does the penny ultimately dwarf the million-dollar lump sum? Because the million remains static. The penny, fueled by compounding, continuously grows. Each day’s gains become the foundation for even larger gains the next day.
From Pennies to Portfolios: Real-World Applications
The penny challenge is more than a thought experiment. It illustrates the potential of compounding in real-world investing.
- The Rule of 72: This handy rule estimates how long it takes an investment to double. Divide 72 by the annual interest rate. For example, at a 6% annual return, an investment would likely double in approximately 12 years (72 / 6 = 12). Keep in mind, this is a simplification, and actual results may vary.
- Dividend Reinvestment: When you reinvest dividends, you buy more shares, which generate more dividends. This is compounding in action, though the actual growth rate will depend on the specific investment’s performance.
Beyond the Basics: Exploring Compounding Further
- Compound Interest Calculators: Online calculators can help you model different investment scenarios and see the impact of compounding with various interest rates and timeframes.
- Compounding Frequency: The more frequently interest is compounded (daily, monthly, annually), the faster the growth, although the difference can be subtle over longer periods.
The Takeaway: Small Changes, Big Results
The Penny Doubling Challenge vividly demonstrates that consistent, even small, contributions over time can lead to astonishing results, thanks to the power of compound interest. It’s a reminder that long-term thinking and disciplined investing are key to financial success. While the penny example is a simplification, ongoing research in behavioral economics suggests that grasping its underlying principle can significantly influence financial decision-making. Remember, investments are subject to market risk, and past performance doesn’t guarantee future returns. Consult with a qualified financial advisor for personalized advice tailored to your situation.
- Veterans Benefits Evaluations: Maximize Your VA Claim - May 13, 2025
- Elevate Your Healthcare Career: Young Executive Programs Compared - May 13, 2025
- Find Davis Workshop Space for Rent: Your Guide to Success - May 13, 2025
